【線膨張率】気をつけろ！微小変形じゃないときの体積膨張率と線膨張率の関係

微小変形の時と大変形のときでは、体積膨張率と線膨張率の関係が違う。
特に、FEM（有限要素法）を利用して、体積変化を模擬する際は、注意が必要である。

微小変形の時の体積膨張率と線膨張率の関係

微小変形の際は、体積変化も線長変化もどちらも温度に従って線形に膨張するという前提があるため、以下の式が同時に成り立つ

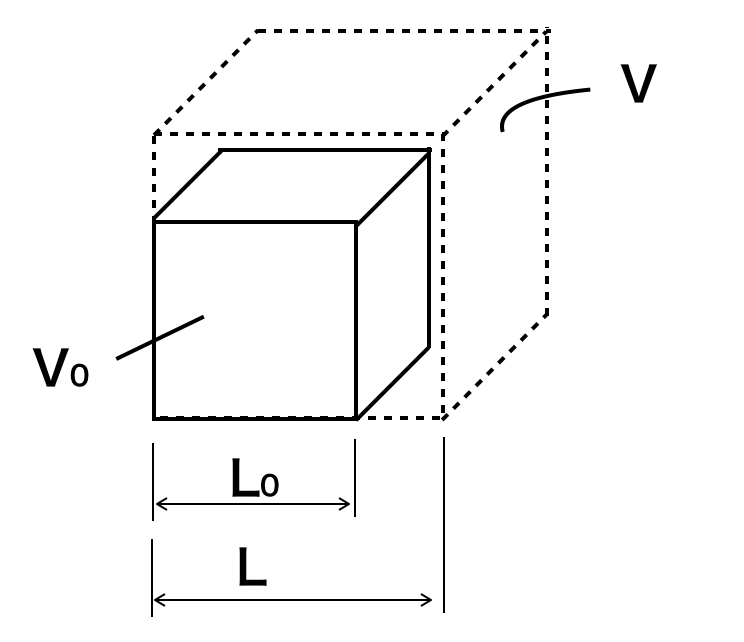
• L=L0+L0αT
• V=V0+V0βT

ここで、L：変形後の線長、L0：変形前の線長、α：線膨張率、T：変化した温度、V:変化後の体積、V0：変化前の体積

上記の式から、

β=3α

となる

大変形のときの体積膨張率と線膨張率の関係

しかし、大変形の時は、先ほどのβが温度に寄らず一定という前提が使えない。
よくよく考えてみると、線長が温度によって線形で増加するとき、体積は線形で膨張する訳ではない。

例えば、α＝0.001で温度が100℃上昇した時（もちろん、実際の固体の膨張率はこんなに高くはないが、FEMで物体を膨張させる時は、温度と線膨張率で膨張を模擬することがある）、

L＝1.1L0

となる。この時の体積は、

V=(1.1L0)^3=(1.1)^3V0=1.331V0

同様に、200℃上昇した時は、

V=(1.2)^3V0=1.728V0

となり、体積は線形に膨張していないことがわかる。つまり、βを一定値とするのが使えない。そこで、変化後の体積変化率B（=βT）とし、次のように定義する

B=(V-V0)/V0=V/V0-1

こうすると、

V0B=V-V0

L0^3B=L^3-L0^3

L0^3 B=L0^3 (1+αT)^3-L0^3

B=(1+αT)^3-1

となる。αを求めるなら

α=1/T ((B+1)^(1/3)-1)

となる。